Young's modulus

Young's modulus, also known as the tensile modulus, is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds.^[1] In solid mechanics, the slope of the stress-strain curve at any point is called the tangent modulus. The tangent modulus of the initial, linear portion of a stress-strain curve is called Young's modulus. It can be experimentally determined from the slope of a stress-strain curve created during tensile tests conducted on a sample of the material. In anisotropic materials, Young's modulus may have different values depending on the direction of the applied force with respect to the material's structure.

It is also commonly called the elastic modulus or modulus of elasticity, because Young's modulus is the most common elastic modulus used, but there are other elastic moduli measured, too, such as the bulk modulus and the shear modulus.

Young's modulus is named after Thomas Young, the 19th century British scientist. However, the concept was developed in 1727 by Leonhard Euler, and the first experiments that used the concept of Young's modulus in its current form were performed by the Italian scientist Giordano Riccati in 1782, predating Young's work by 25 years.^[2]

1 Units
2 Usage
- 2.1 Linear versus non-linear
- 2.2 Directional materials
3 Calculation
4 Approximate values
5 See also
6 References
7 External links

Units

Young's modulus is the ratio of stress, which has units of pressure, to strain, which is dimensionless; therefore, Young's modulus has units of pressure.

The SI unit of modulus of elasticity (E, or less commonly Y) is the pascal (Pa or N/m² or m⁻¹·kg·s⁻²). The practical units used are megapascals (MPa or N/mm²) or gigapascals (GPa or kN/mm²). In United States customary units, it is expressed as pounds (force) per square inch (psi). The abbreviation ksi refers to thousands of psi.

Usage

The Young's modulus calculates the change in the dimension of a bar made of an isotropic elastic material under tensile or compressive loads. For instance, it predicts how much a material sample extends under tension or shortens under compression. Young's modulus is used in order to predict the deflection that will occur in a statically determinate beam when a load is applied at a point in between the beam's supports. Some calculations also require the use of other material properties, such as the shear modulus, density, or Poisson's ratio.

Linear versus non-linear

For many materials, Young's modulus is essentially constant over a range of strains. Such materials are called linear, and are said to obey Hooke's law. Examples of linear materials are steel, carbon fiber and glass. Non-linear materials include rubber and soils, except under very small strains.

Directional materials

Young's modulus is not always the same in all orientations of a material. Most metals and ceramics, along with many other materials, are isotropic, and their mechanical properties are the same in all orientations. However, metals and ceramics can be treated with certain impurities, and metals can be mechanically worked to make their grain structures directional. These materials then become anisotropic, and Young's modulus will change depending on the direction of the force vector. Anisotropy can be seen in many composites as well. For example, carbon fiber has much higher Young's modulus (is much stiffer) when force is loaded parallel to the fibers (along the grain). Other such materials include wood and reinforced concrete. Engineers can use this directional phenomenon to their advantage in creating structures.

Calculation

Young's modulus, E, can be calculated by dividing the tensile stress by the tensile strain in the elastic (initial, linear) portion of the stress-strain curve:

$E \equiv \frac{\mbox {tensile stress}}{\mbox {tensile strain}} = \frac{\sigma}{\varepsilon}= \frac{F/A_0}{\Delta L/L_0} = \frac{F L_0} {A_0 \Delta L}$

where

E is the Young's modulus (modulus of elasticity)

F is the force exerted on an object under tension;

A₀ is the original cross-sectional area through which the force is applied;

ΔL is the amount by which the length of the object changes;

L₀ is the original length of the object.

Force exerted by stretched or compressed material

The Young's modulus of a material can be used to calculate the force it exerts under specific strain.

$F = -\frac{E A_0 \Delta L} {L_0}$

where F is the force exerted by the material when compressed or stretched by ΔL.

Hooke's law can be derived from this formula, which describes the stiffness of an ideal spring:

$F = -\left( \frac{E A_0} {L_0} \right) \Delta L = -k x \,$

where

$k = \begin{matrix} \frac {E A_0} {L_0} \end{matrix} \,$

$x = \Delta L. \,$

Elastic potential energy

The elastic potential energy stored is given by the integral of this expression with respect to L:

$U_e = \int {\frac{E A_0 \Delta L} {L_0}}\, d\Delta L = \frac {E A_0} {L_0} \int { \Delta L }\, d\Delta L = \frac {E A_0 {\Delta L}^2} {2 L_0}$

where U_e is the elastic potential energy.

The elastic potential energy per unit volume is given by:

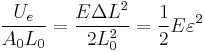$\frac{U_e} {A_0 L_0} = \frac {E {\Delta L}^2} {2 L_0^2} = \frac {1} {2} E {\varepsilon}^2$ , where 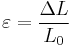$\varepsilon = \frac {\Delta L} {L_0}$ is the strain in the material.

This formula can also be expressed as the integral of Hooke's law:

$U_e = \int {k x}\, dx = \frac {1} {2} k x^2.$

Relation among elastic constants

For homogeneous isotropic materials simple relations exist between elastic constants (Young's modulus E, shear modulus G, bulk modulus K, and Poisson's ratio ν) that allow calculating them all as long as two are known:

$E = 2G(1%2B\nu) = 3K(1-2\nu).\,$

Approximate values

Young's modulus can vary somewhat due to differences in sample composition and test method. The rate of deformation has the greatest impact on the data collected, especially in polymers. The values here are approximate and only meant for relative comparison.

Approximate Young's modulus for various materials^[3]
Material	GPa	lbf/in² (psi)
Rubber (small strain)	0.01–0.1	500–15,000
PTFE (Teflon)	0.5	75,000
Low density polyethylene^[4]	0.238	34,000
HDPE	0.8
Polypropylene	1.5-2	217,000–290,000
Bacteriophage capsids^[5]	1–3	150,000–435,000
Polyethylene terephthalate	2-2.7
Polystyrene	3-3.5	435,000–505,000
Nylon	2–4	290,000–580,000
Diatom frustules (largely silicic acid)^[6]	0.35–2.77	50,000–400,000
Medium-density fiberboard^[7]	4	580,000
Pine wood (along grain)	9	1,300,000
Oak wood (along grain)	11	1,600,000
Human Cortical Bone^[8]	14	2,030,000
High-strength concrete (under compression)	30	4,350,000
Hemp fiber ^[9]	35
Magnesium metal (Mg)	45	6,500,000
Flax fiber ^[10]	58
Aluminium	69	10,000,000
Stinging nettle fiber ^[11]	87
Glass (see chart)	50–90
Aramid^[12]	70.5–112.4
Mother-of-pearl (nacre, largely calcium carbonate) ^[13]	70	10,000,000
Tooth enamel (largely calcium phosphate)^[14]	83	12,000,000
Brass and bronze	100–125	17,000,000
Titanium (Ti)		16,000,000
Titanium alloys	105–120	15,000,000–17,500,000
Copper (Cu)	117	17,000,000
Glass-reinforced plastic (70/30 by weight fibre/matrix, unidirectional, along grain)	40–45	5,800,000–6,500,000
Glass-reinforced polyester matrix ^[15]	17.2	2,500,000
Carbon fiber reinforced plastic (50/50 fibre/matrix, unidirectional, along grain)	125–150	18,000,000–22,000,000
Carbon fiber reinforced plastic (70/30 fibre/matrix, unidirectional, along grain)^[16]	181	26,300,000
Silicon single crystal, different directions ^[17]	130-185
Wrought iron	190–210
Steel	200	29,000,000
polycrystalline Yttrium iron garnet (YIG)^[18]	193	28,000,000
single-crystal Yttrium iron garnet (YIG)^[19]	200	30,000,000
Beryllium (Be)	287	42,000,000
Molybdenum (Mo)	329
Tungsten (W)	400–410	58,000,000–59,500,000
Sapphire (Al₂O₃) along C-axis	435	63,000,000
Silicon carbide (SiC)	450	65,000,000
Osmium (Os)	550	79,800,000
Tungsten carbide (WC)	450–650	65,000,000–94,000,000
Single-walled carbon nanotube^[20]^[21]	1,000+	145,000,000+
Graphene	1000
Diamond (C)^[22]	1220	150,000,000–175,000,000

References

^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "modulus of elasticity (Young's modulus), E".
^ The Rational Mechanics of Flexible or Elastic Bodies, 1638–1788: Introduction to Leonhardi Euleri Opera Omnia, vol. X and XI, Seriei Secundae. Orell Fussli.
^ http://www.engineeringtoolbox.com/young-modulus-d_417.html
^ http://www.matweb.com/search/datasheet.aspx?MatGUID=557b96c10e0843dbb1e830ceedeb35b0
^ Ivanovska IL, de Pablo PJ, Sgalari G, MacKintosh FC, Carrascosa JL, Schmidt CF, Wuite GJL (2004). "Bacteriophage capsids: Tough nanoshells with complex elastic properties". Proc Nat Acad Sci USA. 101 (20): 7600–5. Bibcode 2004PNAS..101.7600I. doi:10.1073/pnas.0308198101. PMC 419652. PMID 15133147. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=419652.
^ Subhash G, Yao S, Bellinger B, Gretz MR. (2005). "Investigation of mechanical properties of diatom frustules using nanoindentation". J Nanosci Nanotechnol. 5 (1): 50–6. doi:10.1166/jnn.2005.006. PMID 15762160.
^ Material Properties Data: Medium Density Fiberboard (MDF)
^ Rho, JY (1993). "Young's modulus of trabecular and cortical bone material: ultrasonic and microtensile measurements". Journal of Biomechanics 26 (2): 111-119.
^ Nabi Saheb, D.; Jog, JP. (1999). "Natural fibre polymer composites: a review". Advances in Polymer Technology 18 (4): 351–363. doi:10.1002/(SICI)1098-2329(199924)18:4<351::AID-ADV6>3.0.CO;2-X.
^ Bodros, E. (2002). "Analysis of the flax fibres tensile behaviour and analysis of the tensile stiffness increase". Composite Part A 33 (7): 939–948. doi:10.1016/S1359-835X(02)00040-4.
^ Bodros, E.; Baley, C. (15 May 2008). "Study of the tensile properties of stinging nettle fibres (Urtica dioica)". Materials Letters 62 (14): 2143–2145. doi:10.1016/j.matlet.2007.11.034.
^ DuPont (2001). Kevlar Technical Guide. p. 9.
^ A. P. Jackson,J. F. V. Vincent and R. M. Turner (1988). "The Mechanical Design of Nacre". Proc. R. Soc. Lond. B 234 (1277): 415–440. Bibcode 1988RSPSB.234..415J. doi:10.1098/rspb.1988.0056. http://rspb.royalsocietypublishing.org/content/234/1277/415.abstract.
^ M. Staines, W. H. Robinson and J. A. A. Hood (1981). "Spherical indentation of tooth enamel". Journal of Materials Science. http://www.springerlink.com/content/w125706571032231/.
^ Polyester Matrix Composite reinforced by glass fibers (Fiberglass). [SubsTech] (2008-05-17). Retrieved on 2011-03-30.
^ Epoxy Matrix Composite reinforced by 70% carbon fibers [SubsTech]. Substech.com (2006-11-06). Retrieved on 2011-03-30.
^ Physical properties of Silicon (Si). Ioffe Institute Database. Retrieved on 2011-05-27.
^ Chou, H. M.; Case, E. D. (November, 1988). "Characterization of some mechanical properties of polycrystalline yttrium iron garnet (YIG) by non-destructive methods". Journal of Materials Science Letters 7 (11): 1217–1220. doi:10.1007/BF00722341.
^ YIG properties
^ L. Forro et al.. "Electronic and mechanical properties of carbon nanotubes". http://ipn2.epfl.ch/CHBU/papers/ourpapers/Forro_NT99.pdf.
^ Y.H.Yang et al.; Li, W. Z. (2011). "Radial elasticity of single-walled carbon nanotube measured by atomic force microscopy". Applied Physics Letters 98 (4): 041901. Bibcode 2011ApPhL..98d1901Y. doi:10.1063/1.3546170.
^ Spear and Dismukes (1994). Synthetic Diamond – Emerging CVD Science and Technology. Wiley, NY. ISBN 9780471535898.

External links

Branches of physics

Elastic moduli for homogeneous isotropic materials

Bulk modulus ( $K$ ) · Young's modulus ( $E$ ) · Lamé's first parameter ( $\lambda$ ) · Shear modulus ( $G$ ) · Poisson's ratio ( $\nu$ ) · P-wave modulus ( $M$ )

Conversion formulas
Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these, thus given any two, any other of the elastic moduli can be calculated according to these formulas.
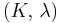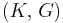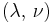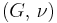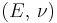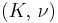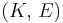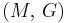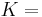	$(\lambda,\,G)$	$(E,\,G)$	$(K,\,\lambda)$	$(K,\,G)$	$(\lambda,\,\nu)$	$(G,\,\nu)$	$(E,\,\nu)$	$(K,\, \nu)$	$(K,\,E)$	$(M,\,G)$
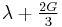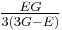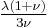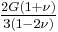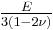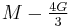$K=\,$	$\lambda%2B \tfrac{2G}{3}$	$\tfrac{EG}{3(3G-E)}$			$\tfrac{\lambda(1%2B\nu)}{3\nu}$	$\tfrac{2G(1%2B\nu)}{3(1-2\nu)}$	$\tfrac{E}{3(1-2\nu)}$			$M - \tfrac{4G}{3}$
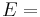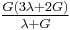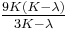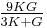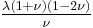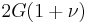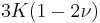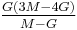$E=\,$	$\tfrac{G(3\lambda %2B 2G)}{\lambda %2B G}$		$\tfrac{9K(K-\lambda)}{3K-\lambda}$	$\tfrac{9KG}{3K%2BG}$	$\tfrac{\lambda(1%2B\nu)(1-2\nu)}{\nu}$	$2G(1%2B\nu)\,$		$3K(1-2\nu)\,$		$\tfrac{G(3M-4G)}{M-G}$
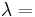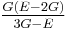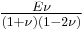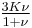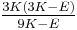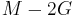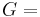$\lambda=\,$		$\tfrac{G(E-2G)}{3G-E}$		$K-\tfrac{2G}{3}$		$\tfrac{2 G \nu}{1-2\nu}$	$\tfrac{E\nu}{(1%2B\nu)(1-2\nu)}$	$\tfrac{3K\nu}{1%2B\nu}$	$\tfrac{3K(3K-E)}{9K-E}$	$M - 2G\,$
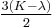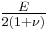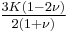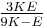$G=\,$			$\tfrac{3(K-\lambda)}{2}$		$\tfrac{\lambda(1-2\nu)}{2\nu}$		$\tfrac{E}{2(1%2B\nu)}$	$\tfrac{3K(1-2\nu)}{2(1%2B\nu)}$	$\tfrac{3KE}{9K-E}$
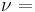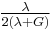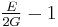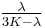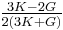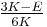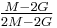$\nu=\,$	$\tfrac{\lambda}{2(\lambda %2B G)}$	$\tfrac{E}{2G}-1$	$\tfrac{\lambda}{3K-\lambda}$	$\tfrac{3K-2G}{2(3K%2BG)}$					$\tfrac{3K-E}{6K}$	$\tfrac{M - 2G}{2M - 2G}$
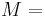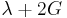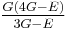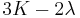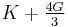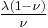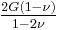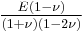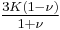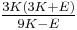$M=\,$	$\lambda%2B2G\,$	$\tfrac{G(4G-E)}{3G-E}$	$3K-2\lambda\,$	$K%2B\tfrac{4G}{3}$	$\tfrac{\lambda(1-\nu)}{\nu}$	$\tfrac{2G(1-\nu)}{1-2\nu}$	$\tfrac{E(1-\nu)}{(1%2B\nu)(1-2\nu)}$	$\tfrac{3K(1-\nu)}{1%2B\nu}$	$\tfrac{3K(3K%2BE)}{9K-E}$
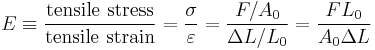
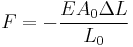
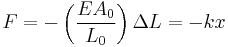
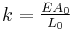
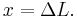
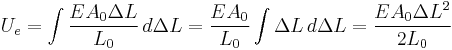
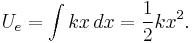
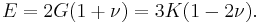